
( p is the momentum of the object, m is the object's mass, and v is the velocity of the object) so He combined Planck's constant and linear momentum He assumed that all moving objects have wave-like properties.

Since both particle and wave theories of light seem to explain a portion of light properties correctly, which is the correct one? In 1924, de Broglie (1892-1987) proposed an answer to this question. This helps explain the blackbody radiation observation.
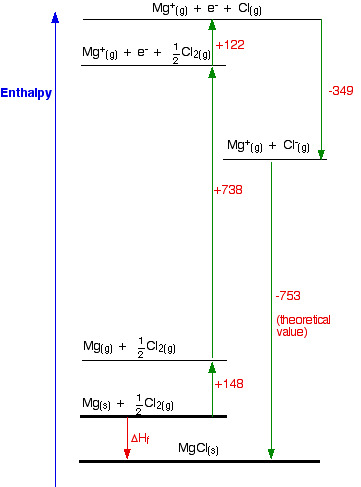
Figure 2Īccording to Particle theory of light, light energy will increase to a discreet and finite value unless λ goes to zero, which will never happen according to the Particle in a One-Dimensional Box theory. The photoelectric effect shows that light behaves like a photon or a particle packed with energy, in other words light waves behave like particles.
#LATTICE ENERGY EQUATION KE PLUS#
We can rewrite the equation to show that the total energy is equal to Φ plus the kinetic energy The threshold energy is the amount of energy needed to eject an electron, and is called work function Φ. Einstein explained that in the photoelectric effect energy each photon's energy is absorbed by one electrons in a given metal, and as a result the electron was able to eject if the photon's energy is equal or greater than the threshold energy (Figure 2). The total energy of a system is equal to the kinetic energy plus the potential energy, and as always the Law of Conservation of energy applies. In 1905, Einstein assumed that Planck’s discrete energies are packets of energy called photons. Replace v=c/λ into the above equation, we have Hence, he stated that if x number of particles were present with a certain frequency value, than energy would beįrequency is related to the wavelength where c= vλ or v=c/λ Quantization of energy states that there are discrete values or states, and energies in between the values of n are forbidden. (where n is an integer, and can be zero or a positive number). He also formulated the quantum theory by saying that light that was emitted had discrete levels of energy, and that energy that was radiated was quantized Where h is Planck’s constant 6.626x10 -34 J.S and v is the frequency. Using blackbody radiator (equal emitter and absorber of radiation at all wavelengths), Planck derived the equation for the smallest amount of energy that can be changed into light The first experiments towards Wave-Particle duality were done by German Physicist Max Planck (1858-1947).

By summing up the energies of interaction between all the ions in the crystal lattice, we can determine the strength of the ionic bonds in the compound.\) In conclusion, the lattice energy of KCl can be calculated using Coulomb's law and considering the distance between the ions and their charges. Given that n = 9 and A = 1.746, we can substitute the values into the equation:Ĭalculating the above expression gives us the lattice energy of KCl. Where n is the number of ions in the formula unit of the compound. Since KCl has a 1:1 ratio of K+ and Cl- ions, the lattice energy can be written as: The lattice energy is the sum of the energies of interaction between all the ions in the crystal lattice. Given that k is a constant and Q1 = +1 for K+ and Q2 = -1 for Cl-, the equation simplifies to:

Using Coulomb's law, we can calculate the energy of interaction between the K+ and Cl- ions: Calculate the energy of interaction between the ions: Given that a = 628 pm, which is the sum of the ionic radii, we can calculate the distance between the ions as follows:Ģ. The distance between the ions, denoted as r, can be determined using the ionic radii of K+ and Cl- ions. The lattice energy can be calculated by summing up the energies of interaction between all the ions in the crystal lattice.ġ. In the case of KCl, we have K+ and Cl- ions. Where E is the energy of interaction, k is a proportionality constant, Q1 and Q2 are the charges of the particles, and r is the distance between them. Mathematically, Coulomb's law can be written as: To calculate the lattice energy of KCl, we need to consider the various factors that contribute to the overall energy.Ĭoulomb's law states that the energy of interaction between two charged particles is directly proportional to the product of their charges and inversely proportional to the distance between them. It is a measure of the strength of the ionic bonds in the compound. The lattice energy of an ionic compound is the energy required to separate one mole of the solid into its constituent ions in the gas phase. **Calculating the Lattice Energy of KCl**


 0 kommentar(er)
0 kommentar(er)
